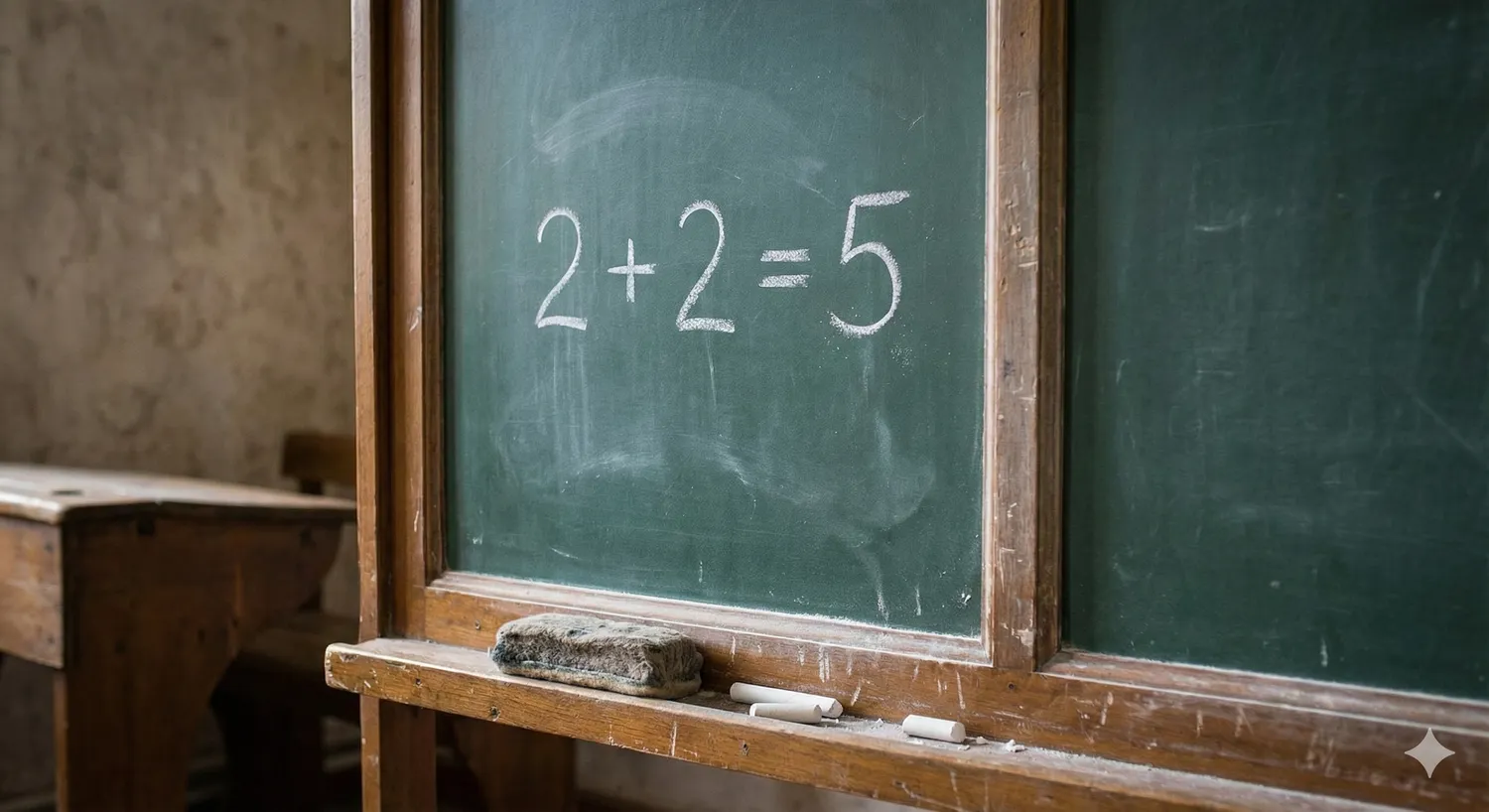Iš pirmo žvilgsnio tai skamba kaip visiška nesąmonė. 2 + 2 yra vienas pirmųjų dalykų, kuriuos išmokstame mokykloje, ir atsakymas atrodo neginčijamas – 4. Tačiau mokslininkai, matematikai ir statistikai jau seniai naudoja šią formulę ne kaip klaidą, o kaip provokaciją. Ji skirta parodyti, kaip stipriai kontekstas, apibrėžimai ir prielaidos gali pakeisti tai, ką laikome „akivaizdžia tiesa“.
Problema slypi ne matematikoje, o kontekste
Matematikoje, griežtai laikantis aksiomų, 2 + 2 visada lygu 4. Tačiau realus pasaulis retai paklūsta idealioms matematinėms abstrakcijoms. Skaičiai, kuriuos naudojame kasdien, yra tik supaprastinti tikrovės modeliai.
Biostatistikas Kareemas Carras dar 2020 metais sukėlė didelę diskusiją socialiniuose tinkluose, parašęs, kad jei kas nors sako „2 + 2 = 5“, pirmas klausimas turėtų būti ne pasipiktinimas, o labai paprastas dalykas: kokie apibrėžimai ir kokios taisyklės čia naudojamos?
Jo mintis buvo aiški – skaičiai patys savaime neegzistuoja. Jie yra mūsų sukurti simboliai, skirti aprašyti realius reiškinius. O kai pasikeičia kontekstas, keičiasi ir tai, ką tie simboliai reiškia.
Kai matematika susiduria su tikrove
Įsivaizduokite paprastą pavyzdį: į du puodelius kepimo sodos įpilate du puodelius acto. Cheminės reakcijos metu gaunate daugiau nei keturis puodelius putojančios masės, nes atsiranda dujos ir keičiasi tūris. Ar tai reiškia, kad 2 + 2 tapo 5? Ne matematikos prasme, bet fizinės realybės požiūriu – taip, rezultatas nebeatitinka paprasto sudėjimo.
Panašiai nutinka ir kitur. Kampų matematikoje 360 laipsnių kampas yra tas pats, kas 0 laipsnių – jų orientacija sutampa. Jei prie kampo nuolat pridedate laipsnius, galiausiai „grįžtate“ į tą pačią padėtį. Taigi rezultatas priklauso ne tik nuo skaičių, bet ir nuo to, kaip juos interpretuojate.
Net apvalinimas gali „sugadinti“ aritmetiką. Du skaičiai 2,3 suapvalinami iki 2. Tačiau 2,3 + 2,3 = 4,6, o tai jau suapvalinus tampa 5. Skaičiai tie patys, veiksmas tas pats, bet rezultatas – kitas.
Skaičiavimas nėra toks „natūralus“, kaip manome
Dar viena svarbi detalė – žmonės nėra „gimę“ mokėdami skaičiuoti. Maži vaikai pirmiausia išmoksta atpažinti mažus kiekius – tai vadinama subitizavimu. Pavyzdžiui, mes iš karto matome, kad ant stalo yra trys obuoliai, bet didesnius kiekius jau turime skaičiuoti sąmoningai.
Net gyvūnai, galintys atskirti keturis ar penkis objektus, laikomi išskirtiniais. Tai rodo, kad skaičiai yra ne prigimtinė realybės dalis, o žmogaus sukurta sistema. Todėl, kai šią sistemą bandome pritaikyti sudėtingiems, kintantiems reiškiniams, neišvengiamai atsiranda įtampa.
Toliau skaitykite kitame puslapyje.